Определение основных технико-эксплуатационных показателей по маршрутам перевозки

3) А3Б3-Б3А2-А2Б4-Б4А3,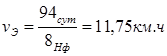

Эксплуатационное количество автомобилей по маршруту

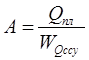, (3.15)

где Qпл – плановое число тонн, которое необходимо перевезти по маршруту

1) А1Б1-Б1А1,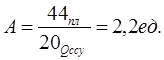

2) А1Б2-Б2А1,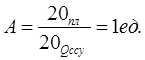

3) А3Б3-Б3А2-А2Б4-Б4А3,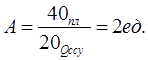

Определяем количество автомобиле-часов в наряде на маршруте за сутки

(3.16)

1) А1Б1-Б1А1,

2) А1Б2-Б2А1,

3) А3Б3-Б3А2-А2Б4-Б4А3,

3.4.1.12 Определяем автомобиле-дни в эксплуатации по маршруту

(3.17)

1) А1Б1-Б1А1,

2) А1Б2-Б2А1,

3) А3Б3-Б3А2-А2Б4-Б4А3,

Определяем общий пробег автомобилей по маршруту за расчётный период

(3.19)

1) А1Б1-Б1А1,

2) А1Б2-Б2А1,

3) А3Б3-Б3А2-А2Б4-Б4А3,

Определяем груженный пробег автомобилей по маршруту за расчётный период

(3.20)

1) А1Б1-Б1А1,

2) А1Б2-Б2А1,

3) А3Б3-Б3А2-А2Б4-Б4А3,

3.4.1.15 Объём перевозок в тоннах за рассматриваемый период

(3.21)

1) А1Б1-Б1А1,

2) А1Б2-Б2А1,

3) А3Б3-Б3А2-А2Б4-Б4А3,

Суточная производительность автомобиля в т.км

WPСУТ=nк*Zоб*qк*(YК1+YК2+….+YКn)+Wксут*Gк *(YК1+YК2+….+YКn) (3.22)

А1Б1-Б1А1,

WPСУТ=8к*4об*0,375к*(0,8к*15ег)+32ксут*0,250к *15К=264 т.км.

2) А1Б2-Б2А1, WPСУТ =

= 8к*4об*0,375к*(0,8к*17ег)+32ксут*0,250к*17К=136 т.км.

3) А3Б3-Б3А2-А2Б4-Б4А3

WPСУТ=8к*2об*0,375к*(0,8к*13ег1+0,8к*17ег2)+32ксут*0,25к*(13ег1+17ег2)=240 т.км.

Определяем грузооборот, т.км

(3.23)

1) А1Б1-Б1А1,

2) А1Б2-Б2А1,

3) А3Б3-Б3А2-А2Б4-Б4А3,

Популярное на сайте:

Анализ грузопотока между Россией Южной Америкой
У России со странами Южной Америки всегда были отлично налажены экономические отношения. Однако целесообразными поставки из Южной Америки в основном стали относительно недавно, после появления прямого морского грузового маршрута в Россию. Ранее приходилось направлять грузы транзитом через другие по ...

Инструмент и детали используемые в рихтовочных работах
Правочные рычаги и прижимы необходимы для восстановления деформированных поверхностей в труднодоступных местах. Прежде чем приступить к выполнению правки какой-либо поверхности, удалите все наладки, молдинги, обивку и другие навесные детали из района повреждения. При наличии люков, обеспечивающих д ...

Оперативно-суточное планирование и управление перевозками грузов
Работа по оперативно-суточному планированию, управлению перевозками грузов и контролю за работой подвижного состава возлагается на службу эксплуатации автотранспортного предприятия (или другое структурное подразделение, ее заменяющее). Оперативно-суточное планирование и контроль за перевозками вклю ...