Расчет числовых характеристик распределения случайных величин

Более полное, а главное, обобщенное представление о результатах эксперимента дают не абсолютные, а относительные (удельные) значения полученных данных. Так, вместо абсолютных значений числа экспериментальных данных ni, целесообразно подсчитать долю рассматриваемых событий в интервале, приходящихся на одно изделие (деталь, узел, агрегат или автомобиль) из числа находящихся под наблюдением, т.е. на единицу выборки. Эта характеристика экспериментального распределения называется относительной частотой (частостью) mi появления данного события (значений признака Xi):

.

Относительная частота mi при этом, в соответствии с законом больших чисел, является приближенной экспериментальной оценкой вероятности появления события .

Значения экспериментальных точек интегральной функции распределения рассчитывают как сумму накопленных частостей mi в каждом интервале Ki. В первом интервале во втором интервале

и т.д., т.е.

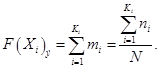
Таким образом, значение изменяются в интервале [0;1] и однозначно определяют распределение относительных частот в интервальном вариационном ряду.

Другим удельным показателем экспериментального распределения является дифференциальная функция , определяемая как отношение частости к длине интервала

и характеризующая долю рассматриваемых событий в интервале, приходящуюся на одно испытываемое изделие и на величину ширины интервала. Функция также еще называется плотностью вероятности распределения.

Полученные результаты расчета сводим в статистическую таблицу.

Таблица 2

Результаты интервальной обработки экспериментальных данных.

Популярное на сайте:

Расчет показателей обслуживания пассажиров в справочном бюро вокзала
Показатели обслуживания пассажиров в справочном бюро вокзала - количество окон, обеспечивающих предоставление необходимого числа справок, длина очереди и ассортимент справок. В курсовом проекте они определяются для вокзала станции А. Число окон справочного бюро вокзала зависит от классности вокзала ...

Обыкновенный стрелочный перевод
Форма остряков в плане определяется требованием обеспечения наилучших условий взаимодействия подвижного состава и элементов стрелочного перевода в зоне стрелки. При этом, важнейшим требованием является обеспечение плавного перехода подвижного состава с прямого участка на стрелку и далее на переводн ...

Разработка комплекта технологической документации на ремонт дефектов блока цилиндров двигателя ЗМЗ-23Д
Разработка технологических процессов ремонта узлов и агрегатов автомобилей производится с учетом требований технических условий, которые являются основным документом, регламентирующим качество, объем трудовых затрат, расходы на запасные части и материалы, необходимые для ремонта. Технологическую до ...