Расчет потерь давления в напорной и сливной гидролиниях

Путевые потери давления определяем по формулам (3.8.1) и (3.8.2)

(3.8.1)

Где ΔРП.Н. – потери давления в напорной гидролинии, МПа;

ΔРП.С. – потери давления в сливной гидролинии, МПа.

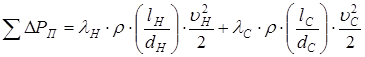(3.8.2)

Где λН, λС – коэффициенты трения жидкости в напорной и сливной гидролиниях;

lН, 1С – длины напорной и сливной гидролиний, м;

dH, dС – диаметры напорной и сливной гидролиний, м;

υH, υС - скорости потока жидкости в напорном и сливном трубопроводах, м/с;

ρ – плотность жидкости, кг/м3.

Как и при расчете давления во всасывающем трубопроводе, занесем все переменные параметры в таблицу (3.8.1), полученные из графиков или расчетным путем.

По графику зависимости поправочного коэффициента b от числа Рейнольдса находим поправочные коэффициенты bН и bC для напорной и сливной гидролинии.

Рассчитаем путевые потери давления в напорном и сливном трубопроводах:

При температуре жидкости tЖ = 0°С

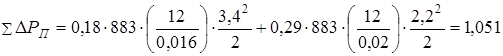МПа

Местные потери давления определяем по формулам (3.8.3) и (3.8.4)

, (3.8.3)

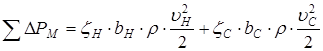(3.8.4)

Где ζН и ζС - коэффициенты местных сопротивлений в напорном и сливном трубопроводах;

bH и bC - поправочные коэффициенты, учитывающие влияние вязкости жидкости на местные потери давления в напорном и сливном трубопроводах;

υH и υC - скорости потока жидкости в напорном и сливном трубопроводах, м/с;

ρ - плотность жидкости, кг /м3.

Определим число Рейнольдса при температуре tж = 20 ˚С для напорного и сливного трубопровода по формулам (3.8.5) и (3.8.6)

, (3.8.5)

(3.8.6)

Аналогичными расчетами определим число Рейнольдса и для других температур и результаты расчета занесем в таблицу (3.8.1).

Определим коэффициенты гидравлического трения для напорного и сливного трубопроводов. Результаты занесем в таблицу (3.8.1).

При температуре жидкости tж = 20 ˚С:

,

,

.

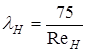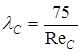
Рассчитаем местные потери давления при температуре рабочей жидкости tж = 20 ˚С:

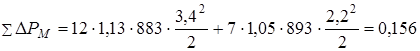МПа.

На основании расчетных данных строим график (рисунок 3.8.1)

Таблица 3.8.1 – Зависимость потерь давления в гидросистеме экскаватора от температуры рабочей жидкости.

Популярное на сайте:

Определение потребного числа ячеек в автоматических камерах хранения
На вокзале станции А для периода максимальных перевозок с учетом внутрисуточной неравномерности прибытия пассажиров определяют потребное число ячеек в автоматической камере хранения (КХС): , (3.12) где - максимальное число пассажиров, пользующихся услугами КХС; - доля пассажиров, обращающихся в КХС ...

Документация производственного участка по охране труда и пожарной безопасности, предупредительные надписи на рабочих местах
Документацией производственного участка является «Инструктаж по охране труда на автотранспортном предприятии ООО «Котласский ЛДК»» На рабочих местах существуют следующие предупредительные надписи: при обслуживании АТС на подъемнике (гидравлическом, электромеханическом) – надпись «Не трогать – под а ...

Расчет тихоходной цилиндрической зубчатой передачи
Исходные данные: Число смен 3; режим работы с(р); срок службы 4 года. Определение режима работы зубчатых колес. Определяем коэффициент долговечности по контактной прочности: где: Определяем наработку: где: - машинное время работы. где: . часов. циклов. Определяем коэффициент долговечности по изгибу ...